Lately I’ve been doing quite a lot of travelling across South Africa, visiting many smaller cities in the provinces. Because of this I was inspired to revisit and improve a project from earlier this year in which I produced an isochrone map of South Africa showing travel time from Johannesburg.

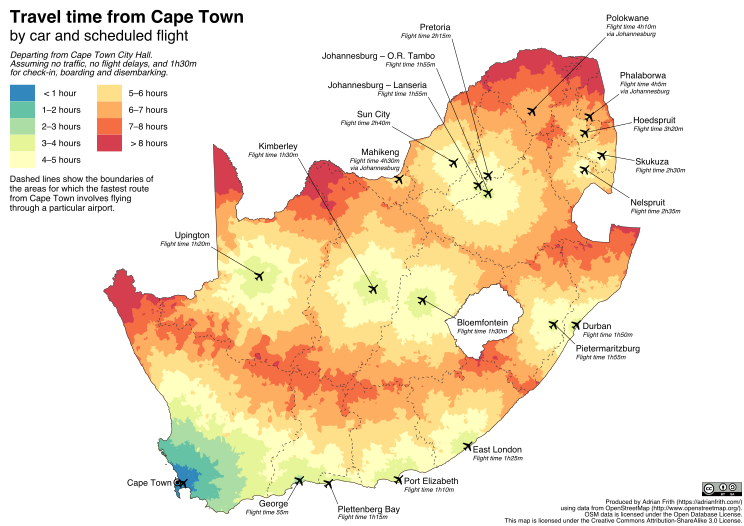
The map below shows how long (approximately) it takes to travel from Johannesburg to any point in South Africa using cars and scheduled airline flights. Specifically, it shows the shortest travel time from Johannesburg City Hall, either by driving directly to the destination, or by driving to OR Tambo International Airport, flying to another airport and then driving to the destination.

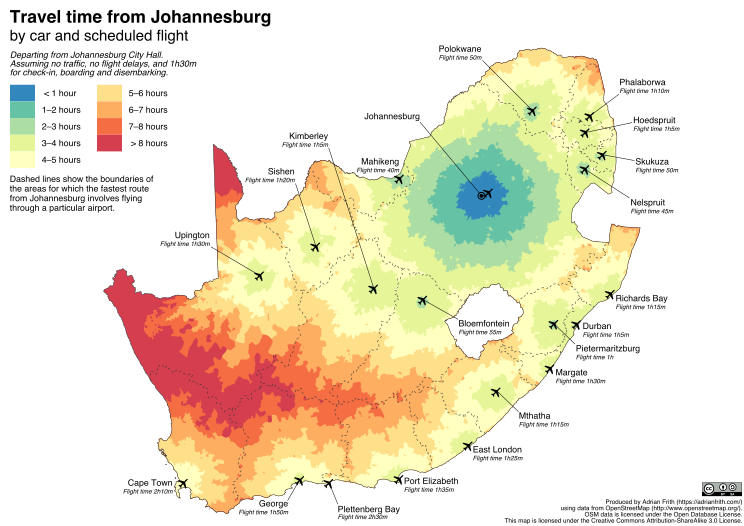
The map also shows (using dashed lines) the “catchment area” for each airport, by which I mean the area of the country for which the fastest route from Joburg involves flying to that airport. It makes some optimistic assumptions: that no traffic is encountered on the road; that there are no flight delays; and that a total of 1 hour and 30 minutes is used for checking in and boarding a flight and for disembarking at the other end.

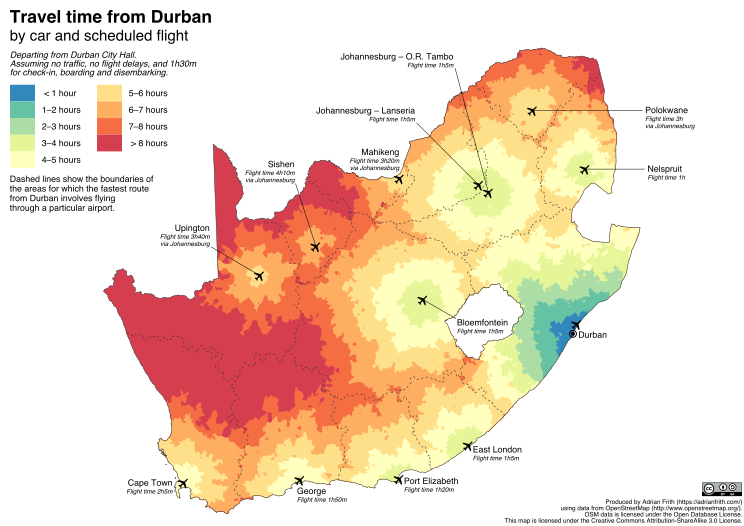
I’ve also made similar maps for travel time from Cape Town and Durban, which can be seen below.

I produced these maps using the pgRouting routing engine and road network data from OpenStreetMap. This post details how I did it; the accompanying code is available on GitHub.

Strategy

The strategy for producing these maps can be briefly described as follows:

1. Calculate the driving time from the origin point (e.g. Johannesburg City Hall) to every point on the road network of South Africa.
2. Calculate the driving time from the origin point to the nearest airport (e.g. OR Tambo International).
3. Look up the flying times for every scheduled route out of that airport.
4. Calculate the driving time from every airport in South Africa to every point on the road network of South Africa.
5. For every point on the road network, work out the shortest time travel time out of all all possible routes.
   1. One possible route is the direct drive from the origin which has been calculated in point 1.
   2. Another possible route is given by each flight route out of the airport identified in point 3. The time for each of those routes is given by adding up the driving time from the origin from point 2, the flight time from point 3, the driving time to the destination from point 4, and an extra 90 minutes to account for check-in, boarding, disembarking, etc.

One caveat regarding point 3: every airport in South Africa that is served by scheduled flights has flights from OR Tambo, so it’s unnecessary to consider flights from other airports (e.g. Lanseria or Wonderboom). When it comes to Cape Town and Durban, each city is served by only one airport, but they don’t have direct flights to all airports, so you have to consider routes that involve changing planes in Johannesburg.

Implementation

If you want to follow along on your computer, you’ll need to install some software:

• PostgreSQL
• PostGIS
• pgRouting
• osm2pgrouting

On my Mac I installed all of these with Homebrew by running

brew install postgresql postgis pgrouting osm2pgrouting

On another OS, you’re on your own; I’m pretty sure they’re all available through apt on a Debian or Ubuntu system.

Create the database and load the SA road network

First we create a PostgreSQL database, and add the PostGIS and pgRouting extensions. I’ve called the database traveltime.

createdb traveltime
psql traveltime -c "create extension postgis"
psql traveltime -c "create extension pgrouting"

Then we download and unzip the South African OpenStreetMap extract graciously provided by GeoFabrik.

wget http://download.geofabrik.de/africa/south-africa-latest.osm.bz2
bunzip2 south-africa-latest.osm.bz2

Next we load the OSM data into the pgRouting database. You will need to change the username from adrian to your username. The mapconfig.xml file, which describes the features to load from the OSM data, is available from the git repository.

osm2pgrouting --f south-africa-latest.osm --conf mapconfig.xml \
 --dbname traveltime --username adrian --clean

Remove unconnected ways and vertices

From here on, everything we do is going to be inside the PostgreSQL shell, which we start by running something like the following.

psql traveltime

The database produced by osm2pgrouting has two main tables: ways, which contains road segments; and ways_vertices_pgr, which contains vertices, i.e. points where two or more road segments meet.

In the OSM extract there are some ways and vertices that are not connected to the main South African road network, meaning that they will never be reachable from our origin point or from an airport. We want to remove these from the database so that they won’t complicate things later. First we produce a list of all the vertices that are connected to the network.

CREATE TEMP TABLE connected_vertex (
    id bigint PRIMARY KEY
);

INSERT INTO connected_vertex (id)
SELECT node
FROM pgr_drivingDistance(
    'SELECT gid AS id, source, target, 1 AS cost, 1 AS reverse_cost FROM ways',
    (SELECT id FROM ways_vertices_pgr WHERE osm_id = 263568563),
    20000
);

This is our first encounter with the pgr_drivingDistance function, and it needs some explaining. This function walks the road network starting at a specified vertex, and calculates the driving distance (or time) from the starting point to each vertex in the network. In this case we don’t care about the driving time; we’re just using it to find out which vertices are connected at all.

The first parameter to the function is a SQL function which defines the “cost” (distance or time) of travelling along each way; since we don’t care about the cost, we set this to 1 for both the forward and reverse directions.

The second parameter is the origin vertex for the walk; the subquery there is to find the ID of the vertext corresponding to OSM node 263568563 which is a point on the N5 just outside of Winburg in the Free State. (This is correct as of July 2017; if you’re visiting this in the future the OSM data might have changed.) The choice of this point is arbitrary; it has to be a point on the South African road network, and I chose Winburg because it’s central.

The third parameter is a limit on the distance that the function will walk before giving up; in this case 20000 is a limit large enough to make sure we’ve walked the whole network.

Now we can continue by deleting the unconnected ways and vertices.

DELETE FROM ways
USING ways_vertices_pgr AS wv
LEFT JOIN connected_vertex cv ON wv.id = cv.id
WHERE ways.source = wv.id
    AND cv.id IS NULL;

DELETE FROM ways_vertices_pgr
USING ways_vertices_pgr AS wv
LEFT JOIN connected_vertex cv ON wv.id = cv.id
WHERE ways_vertices_pgr.id = wv.id
    AND cv.id IS NULL;

Calculate the driving time from the origin point

We create a table to hold the origin vertex for our map.

CREATE TABLE origin (
    name varchar PRIMARY KEY,
    vertex_id bigint UNIQUE REFERENCES ways_vertices_pgr(id)
);

INSERT INTO origin (name, vertex_id)
SELECT 'Johannesburg', id
FROM ways_vertices_pgr
WHERE osm_id = 201596578;

OSM node 201596578 is the corner of Albertina Sisulu Road and Rissik Street in front of the Johannesburg City Hall. We could add records here for other origins, like Cape Town and Durban.

Now we use pgr_drivingDistance to find the driving time from this vertex to every vertex in the road network.

CREATE TABLE origin_driving_time (
    origin_id bigint REFERENCES origin(vertex_id),
    dest_id bigint REFERENCES ways_vertices_pgr(id),
    time_mins float
);
CREATE INDEX origin_driving_time_origin_id ON origin_driving_time(origin_id);
CREATE INDEX origin_driving_time_dest_id ON origin_driving_time(dest_id);

INSERT INTO origin_driving_time(origin_id, dest_id, time_mins)
SELECT from_v, node, agg_cost
FROM pgr_drivingDistance(
    'SELECT gid AS id, source, target, length_m*0.08/maxspeed_forward AS cost, length_m*0.08/maxspeed_backward AS reverse_cost FROM ways',
    (SELECT array_agg(vertex_id) FROM origin),
    2000, true, false
);

This time we’ve used an actual cost function in the first parameter to pgr_drivingDistance. It takes the length of the way in metres divided by the speed limit in kilometres per hour, and multiplies that by a factor of 0.08, which scales it to a time in minutes and increases that time by a third. This increase accounts for the fact that one can’t always drive at the declared maximum speed of a road. I determined it by comparing the results of pgRouting’s calculations with times given by other routing engines (Google Maps, OSRM, etc.)

The array_agg in the second parameter constructs an array of all the vertices in the origin table, so that if there’s more than one the function will calculate driving times for all the possible origins.

Load airports and flying times

We create a table of airport vertices using the list of OSM node IDs from the file airports.csv. These are the IDs of nodes on the road immediately outside the airport terminal; as before, these are valid as of July 2017 but might need to be updated in the future.

CREATE TABLE airport (
    iata char(3) PRIMARY KEY,
    vertex_id bigint UNIQUE REFERENCES ways_vertices_pgr(id)
);

CREATE TEMP TABLE imp_airport (
    iata char(3) PRIMARY KEY,
    osm_id bigint UNIQUE
);

\COPY imp_airport FROM 'airports.csv' WITH CSV HEADER

INSERT INTO airport (iata, vertex_id)
SELECT iata, wv.id
FROM imp_airport i
    JOIN ways_vertices_pgr wv ON i.osm_id = wv.osm_id;

Next we load details of flying times from one airport to another, from the file flying-time.csv. I collected these times from the airline schedules.

CREATE TABLE flying_time (
    from_iata char(3) REFERENCES airport(iata),
    to_iata char(3) REFERENCES airport(iata),
    time_mins int,
    PRIMARY KEY (from_iata, to_iata)
);

\COPY flying_time FROM 'flying-time.csv' WITH CSV HEADER

Calculate driving times from the airports

Just as we created a table of driving times from the origin point, we now create a table of driving times from each airport vertex.

CREATE TABLE airport_driving_time (
    airport_id bigint REFERENCES airport(vertex_id),
    dest_id bigint REFERENCES ways_vertices_pgr(id),
    time_mins float,
    PRIMARY KEY (airport_id, dest_id)
);
CREATE INDEX airport_driving_time_airport_id ON airport_driving_time(airport_id);
CREATE INDEX airport_driving_time_dest_id ON airport_driving_time(dest_id);

INSERT INTO airport_driving_time(airport_id, dest_id, time_mins)
SELECT from_v, node, agg_cost
FROM pgr_drivingDistance(
    'SELECT gid AS id, source, target, length_m*0.08/maxspeed_forward AS cost, length_m*0.08/maxspeed_backward AS reverse_cost FROM ways',
    (SELECT array_agg(vertex_id) FROM (SELECT vertex_id FROM airport ORDER BY vertex_id LIMIT 10) ids),
    2000, true, false
);

INSERT INTO airport_driving_time(airport_id, dest_id, time_mins)
SELECT from_v, node, agg_cost
FROM pgr_drivingDistance(
    'SELECT gid AS id, source, target, length_m*0.08/maxspeed_forward AS cost, length_m*0.08/maxspeed_backward AS reverse_cost FROM ways',
    (SELECT array_agg(vertex_id) FROM (SELECT vertex_id FROM airport ORDER BY vertex_id OFFSET 10 LIMIT 10) ids),
    2000, true, false
);

INSERT INTO airport_driving_time(airport_id, dest_id, time_mins)
SELECT from_v, node, agg_cost
FROM pgr_drivingDistance(
    'SELECT gid AS id, source, target, length_m*0.08/maxspeed_forward AS cost, length_m*0.08/maxspeed_backward AS reverse_cost FROM ways',
    (SELECT array_agg(vertex_id) FROM (SELECT vertex_id FROM airport ORDER BY vertex_id OFFSET 20 LIMIT 10) ids),
    2000, true, false
);

The repeated uses of pgr_drivingDistance with the LIMIT and OFFSET parameters in the subquery are necessary because that function uses more memory if you have more origin vertices. My computer was not able to calculate the driving times from all 24 airports simultaneously, so I split them up into three batches.

Finding the shortest route to every vertex

At this point we have built up all the data we need according to points 1 to 4 of the strategy that I laid out above. Now we can proceed to calculate the shortest route and travel time from our origin to every vertex on the road network.

CREATE TABLE shortest_route_joburg_vertex AS
WITH all_routes AS (
    SELECT 'XXX' AS via_iata, dest_id, time_mins
    FROM origin
        JOIN origin_driving_time odt ON origin.vertex_id = odt.origin_id
    WHERE origin.name = 'Johannesburg'
    UNION
    SELECT va.iata AS via_iata, adt.dest_id,
        odt.time_mins + ft.time_mins + adt.time_mins + 90.0 AS time_mins
    FROM origin
        JOIN origin_driving_time odt ON origin.vertex_id = odt.origin_id
        JOIN airport fa ON odt.dest_id = fa.vertex_id
        JOIN flying_time ft ON fa.iata = ft.from_iata
        JOIN airport va ON ft.to_iata = va.iata
        JOIN airport_driving_time adt ON va.vertex_id = adt.airport_id
    WHERE origin.name = 'Johannesburg'
        AND fa.iata = 'JNB'
)
SELECT DISTINCT ON (dest_id)
    via_iata, dest_id, time_mins
from all_routes
order by dest_id, time_mins;
ALTER TABLE shortest_route_joburg_vertex ADD PRIMARY KEY (dest_id);

The first part of this query, the indented part in the brackets following WITH all_routes AS, is a common table expression (CTE), which is basically a subquery that we can refer to by the name all_routes in the main part of the query that follows. This CTE builds up all possible routes from Joburg to every vertex.